주식 투자에 유용한 액셀 재무함수들(PV, FV, PMT, RATE, XIRR)

0. 들어가며

내 계좌의 연평균수익률은 얼마인지?
'연평균 복리수익률 10%로 10년 투자할 경우 현재 내가 투입한 금액은 얼마가 될지?
매달 갚아야 하는 나의 대출상환금은 얼마인지 등등

 

주식투자나 금융상품에 가입해보면 재무계산기가 필요할 때가 있습니다. 물론 현업에 계신 분들은 재무계산기를 하나쯤은 갖고 계시겠지만, 일반 금융소비자들은 그렇지 않습니다.

하지만 우리에겐 엑셀(EXCEL)이 있습니다. 엑셀 함수 몇 가지만 기억하고 활용할 줄 안다면 보다 손쉽게 위의 궁금증들을 해결할 수 있습니다.

 

오늘은 특히 주식투자와 대출 관련해 자주 사용되는 'FV, PV, PMT, RATE, XIRR' 이 다섯 가지 함수에 관해 예제와 함께 살펴보도록 하겠습니다. 

 

Texas Instruments 사의 BA2 plus 재무계산기

 

 

---

1. 용어 및 기초적인 내용 정리

재무함수는 기본적으로 특정 기간 할인율에 따른 어느 자산의 현재 가치와 미래 가치에 대한 수식이 주를 이룹니다.

본격적으로 함수들을 살펴보기 전, 자주 등장하는 함수 인수(대입 값) 몇 가지를 살펴보겠습니다. 

 

PV: Present Value, 현재 가치입니다.

현재 시점의 투자금 또는 대출금 등이 여기에 들어갑니다.

한 가지 주의할 점은 돈이 나가는 것은 음의 부호(-)를 붙입니다. 즉, 내가 투자한 투자금이나 대출금은 항상 음의 값을 가지게 되고, 따라서 PV란에는 항상 '-'를 추가로 넣어줘야 합니다.

 

FV: Future Value, 미래 가치입니다.

일반적으론 투자가 완료된 시점의 가치를 나타내고, 채권 투자에서는 FV가 액면가(Face Value)로 읽습니다.

 

PMT: Payment, 투자 기간 일정하게 지급되는 금액을 나타냅니다.

주식으로 따지면 배당 금액이 될수도 있고, 채권으로 따지면 쿠폰(이자)에 해당합니다.

 

Rate: Rate, 기간별 이자율입니다.

'숫자%'로 기입하는데, 이때 한 가지 주의할 점은 연율화 된 이자 값을 집어넣어야 합니다.

 

Nper: number of periods, 투자의 총 지급 기간 또는 횟수를 뜻합니다.

채권의 경우 만기에 해당하고, 주식투자의 경우엔 투자 기간이 됩니다. Rate와 마찬기로 이 항목 역시 연 단위로 기입해야 합니다(Nper =1은 1년을 의미)

 

Type: 납입 시점을 나타내는 숫자입니다.

납입 또는 지급 시점이 기간 말이면 '0', 기간 초라면 '1' 값을 넣습니다. 값을 넣지 않고 생략 시엔 '0'으로 간주합니다.

 

기타 참고사항

1) 내가 구하고 싶은 값에 맞는 함수를 사용합니다. 가령 어떤 자산의 미래 가치가 궁금하면 =FV(), 연평균수익률이 궁금하면 =Rate() 함수를 사용합니다. 함수가 많기 때문에 도출하고자 하는 결과 값이 무엇인지 인지하고 있어야 합니다.

 

2) 특정 항목 생략 시 해당 값은 '0'으로 자동 입력됩니다. 

 

3) 불러오고자 하는 함수 입력 후 'Ctrl+a'를 누르면 함수인수를 입력하기 위한 새창이 열립니다
(ex. 특정 셀에 '=PV'를 입력하고 'Ctrl+a' 누름) 

 

이외에도 다른 인수들이 많지만 나머지는 함수를 직접 다루면서 설명하겠습니다.

 

 

---

2. FV

먼저 FV 함수입니다.
고정된 이율(Rate)과 고정된 지급액(Pmt)에 따라 현재 나의 자산 가치(Pv)가 미래의 어떤 가치(FV)를 가지게 될지 계산할 수 있습니다. 

 

예제) 현재 원금 1억을 연평균(복리)수익률 10%로 30년 동안 굴리면 얼마가 될까?(중간 지급액 즉, 배당 및 추가 투자 금액 없다고 가정)

->

풀이는 간단합니다.

Rate = 10%
Nper = 30
PV = -1(단위 억)

를 집어넣습니다 (*Pmt와 Type 생략)

 

=FV(10%, 30,, -1)

연평균 고정적으로 10%의 수익률을 올릴 수 있는 투자처가 있다면, 30년 뒤 1억은 무려 17억이 됩니다.
매년 고정적인 중간 투자금액을 천만원씩 한다면, 30년 뒤에 그 값은 34억 정도로 크게 뜁니다. 

 

---

3. PV

다음은 주로 채권의 현재가치를 계산할 때 자주 사용하는 PV 함수입니다. 
채권의 가격은 미래 벌어들일 이자들과 원금을 현재가치로 할인한 값의 합으로 결정됩니다. 예제를 보시죠.

 

예제) 액면가 1000(원), 표면이율 3%, 만기 10년 그리고 YTM(만기수익률)인 채권의 현재 가격을 구하시오(단, 납입 시점은 기간 말로 계산)

->

사실 이 문제는 함수를 쓰지 않고 한눈에 보고 맞출 수 있습니다. YTM과 표면금리가 3%로 동일한 경우 채권 가격은 액면가와 동일하니까요.

그래도 함수를 써보면 아래와 같습니다.

 

 

Rate에는 YTM 3%를, Nper은 만기 10을, Pmt에는 액면가 1000에 대한 표면금리 3%만큼의 중간 이자 값인 3%*1000을 집어넣습니다. Fv는 액면가 1000 그대로고요.

 

 

각각의 함수 인수가 무엇을 의미하는지만 알고 있다면 계산은 그리 어렵지 않습니다.
자, 그렇다면 YTM이 3%에서 2%로 바뀔 땐 채권 가격이 얼마나 오를까요? 나아가 위의 수식에서 YTM이 
3%->2%로, 2%->1%, 점점 YTM이 하락했을 때 가격의 변화를 보도록 하겠습니다.

 

 

 YTM이 하락할수록 채권의 가격은 상승합니다. 시장에서 요구하는 수익률은 3%보다 아래인데, 내가 들고 있는 채권의 표면금리는 3%나 되니 이 채권의 가치는 1000원보다 높을 수밖에 없습니다.
가격이 증가하는 폭은 금리가 낮아질수록 점점 커집니다(8.98%->9.14%, 9.30%->9.45%)

 

---

4. PMT

PMT함수는 주로 두 가지 상황에서 사용됩니다.

① 대출상환액을 구할 때

② 특정 금액을 모으기 위한 매월 적립 금액 확인하기 위해

 

먼저 ①번 부터 보겠습니다.

예제) 은행에서 2억을 10년간 연이율 4%로 대출한 경우, 나는 '매월' 얼마씩 상환해야 할까?

->

간단한 문제입니다만 인수를 입력할 때 '매월'이라는 표현에 주의해서 기입해야 합니다. 
따라서 납입 기간과 연이율을 월단위로 바꿔서 넣으면, Nper = 10 * 12(1년은 12개월), Rate = 4% / 12(월이율로 쪼개기)

 

 

 

매월 정해진 날짜에 2,024,903원씩 은행에 상환해야 합니다. 이처럼 상환액을 구하기 위해선 Fv 입력은 생략하며, 함수 전체에는 마이너스(-) 부호를 붙여줘야 합니다. 

 

다음 '②특정 금액을 모으기 위한 매월 적립 금액'을 확인하기 위해 PMT함수를 사용하는 상황입니다.
또 다른 예제를 보겠습니다.

 

예제) 10년간 연이율 4%짜리 적금에 투자하여 2억을 모으기로 했다. 나는 매월 얼마씩 적립해야 2억을 모을 수 있을까?

->

위의 예제와 비슷한 것처럼 느껴지지만 사실은 다른 문제입니다.

기간과 이율은 똑같지만, 이번에는 Fv에 2억이라는 값을 대입해야 합니다. 이 문제에서 2억은 현재가 아닌 미래의 목표 금액이니까요.

 

 

 

 

---

5. Rate

Rate함수는 다양하게 쓸 수 있습니다. 크게 두 가지만 기억하시면 됩니다.
① (투자)기간 대비 (투자) 성과 또는 결과에 따른 성장률
② 대출 기간 또는 횟수에 대한 이자율

말이 조금 복잡합니다. 곧바로 ①번 예제부터 보겠습니다.

 

예제) 1억을 투자해 5년 뒤 5억을 만들었다. 이때 나의 연평균 수익(성장)률은?

->

 

풀이는 간단합니다. Pv, Fv 함수에서 다뤘던 내용에서 크게 벗어나지 않습니다.

또한 수익률 계산에도 활용되지만, 말만 조금 바꿔 아래처럼 장기(7년)와 단기(3년) 성장률 계산에도 쓸 수 있습니다.

지난 7년간 Apple의 Fwd. EPS의 변화. 그에 따른 장기 단기 성장률

위 데이터는 지난 7년간 Apple의 Fwd. EPS의 변화값입니다(21년 9월부터 23년 9월까지는 추정치입니다)

 

장기 성장률의 경우 16년 9월부터 23년 9월까지 총 7년의 기간 동안 Pv 2.08이 Fv 5.92가 되었을 때의 Rate를 구할 수 있고, 

단기 성장률의 경우 20년 9월부터 23년 9월까지 총 3년의 기간 동안 Pv 3.28이 Fv 5.92가 되었을 때의 Rate를 구하면 됩니다.

 

*위처럼 Fwd.EPS 데이터를 무료로 열람하는 법은 다음 포스팅에서 다뤘으니 참고하시기 바랍니다.https://hanyes.tistory.com/23

증권사 리포트 무료로 보는 법 - (1) (feat. 와이즈리포트 & 카이로스:미래에셋대우HTS)

 

 

다음은 '② 대출 기간 또는 횟수에 대한 이자율'로 넘어가겠습니다. 예제를 보시죠.

예제) 은행에서 5억을 빌렸다. 매년 1억 1천 만원씩 5년 동안 매년 말에 상환하기로 했다면, 연평균 이율은 얼마나 되는가?

->

대략적인 이자율이 얼마나 되는지 궁금할 때가 있습니다. Rate 함수만 있다면 계산은 간단합니다.

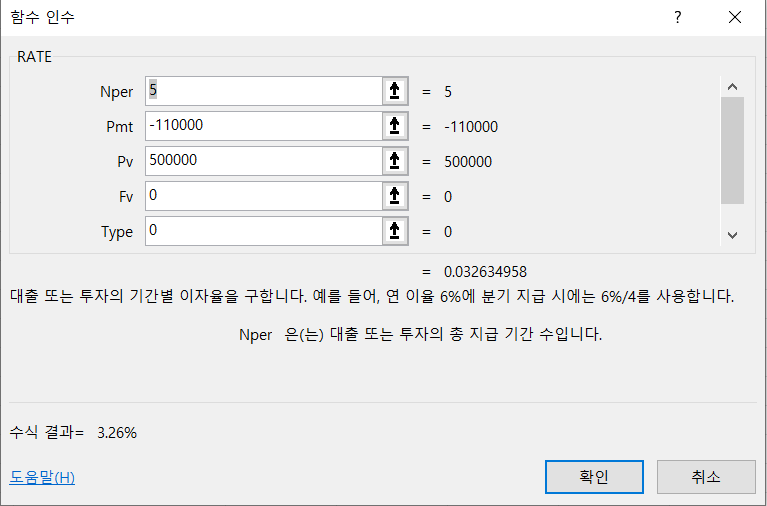
재미 삼아 위와 동일한 조건으로 '연평균' 이율 대신 '월평균' 이율을 구해볼 수 있겠습니다(이때 연 1100만 원을 갚는 것과 동일한 조건 설정을 위해 매달 920만 원 정도를 갚아야 합니다.)

계산해보면 연평균 이율보다 훨씬 낮은 0.33%로 떨어집니다.

 

---

6. XIRR

마지막입니다. XIRR은 특정 기간에 해당하는 수익률을 연율로 환산해주는 놀라운 함수입니다.

시점과 만기에 해당하는 날짜를 '년-월-일'의 형식으로 입력하고, Value를 대입하면 되는데 내 주식계좌의 수익률 계산에 이보다 간편한 함수가 없습니다.

 

먼저, 주가지수의 연평균수익률 계산부터 보시죠.

 

예제) 코스피의 처음 개장 이후 현재까지 코스피의 연평균 수익률은?

->

코스피는 1980년 1월 1일에 '100'으로 시작해 현재(2021년 8월 13일) 종가 '3,171.29'를 기록했습니다.

Values에는 '100'과 '3171.29'에 해당하는 셀 값을 이어 넣고('shift'를 눌러 해당 셀들을 한꺼번에 선택),

Date에는 마찬가지로 1980년과 2021년 현재 시점을 이어 넣습니다.

단, 코스피 시작 값 100은 초기값이므로 '-'부호를 넣습니다.

 

 

*오타입니다. '2021-08-13'이 맞습니다

 

내 주식계좌의 연평균수익률도 XIRR로 계산할 수 있다고 언급했습니다.
투자 시점과 입금 또는 출금 시점을 안다면 정말 쉽게 계산할 수 있습니다.

 

예제) 작년 1월 1일에 100만 원 투자했고, 그로부터 몇 개월 뒤 200만 원을 더 투자했습니다. 그리고 해가 바뀌어 잠시 돈 쓸 일이 생겨 100만 원을 출금했습니다. 그로부터 다시 6개월 뒤 투자했던 금액이 수익이 나서 현재 잔고가 250만 원이 되었습니다. 이때 내 계좌의 연평균수익률은 얼마일까요?(정확한 입출금 날짜는 아래 사진 참고)

 

 

 

정말 간편하지 않니까? 바로 전의 예제처럼 인수에 해당하는 값들을 드르륵 긁어 넣기만 하면 끝입니다. 다만 부호에 주의해야 하며, 날짜를 적은 셀은 위 사진의 형식대로 정확하게 적어야 합니다.

 

---

7. 마치며

이렇게 다섯 가지 함수를 살펴봤습니다. 투자에 있어 정말 많이 사용되는 함수이고, 굉장히 유용한 함수입니다. 

저는 이 함수들의 사용법을 최일 선생님(이안금융교육)께 배웠습니다. 선생님께서 함수를 설명하시며 하셨던 말씀을 끝으로 포스팅을 마치겠습니다. "전쟁터에 나가는 군인이 총기 사용법을 아는 것처럼 투자자라면 반드시 익혀야 하는 것이 바로 액셀 재무함수입니다."